技术分享丨麦克风阵列原理（三）

由于麦克风阵元空间位置的差异，各阵元接收到的信号存在时延，在对信号处理之前进行时延补偿，保证各阵元待处理数据的一致性，使阵列指向期望方向。

考虑最简单的均匀线性麦克风阵列，如图5所示。

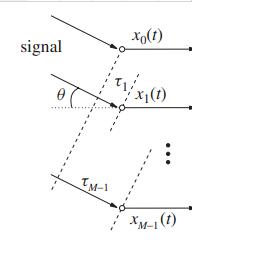
图5ULA时延

设麦克风阵列共用M个阵元，中心为参考点，阵元间距为d，信号入射角为θ，声音传播速度为c，则根据几何知识，第m(0≤m≤M-1)个阵元的时延为τm=(d/c)sinθ(m-(K-1)/2)。

麦克风采集的是数字信号，设采样周期为T，则对时域离散的信号来说，时延为D=τ/T。

通常D不是一个整数，而对离散信号来说，整数时延才有意义。对于非整数D，可以分解为整数部分和分数部分D=⌊D⌋+d，式中，⌊D⌋为D的向下取整，0≤d<1。对于非零的分数部分d，此时信号实际值介于两个相邻采样点之间，即分数延迟。在实际处理中，可对d四舍五入取整，然后加上⌊D⌋，得到近似整数时延，但这种方法处理的结果不够精确。

为了得到较为精确的处理结果，就必须设计分数时延滤波器，对采样信号进行精确的时延补偿。理想的分数时延滤波器的冲激响应可表示为hid(m)=sinc(m-D)。

由数字信号处理知识可知，上式是无限长、非因果不稳定的，在物理上不可实现。为了解决这一问题，在实际操作中，通常会对上式进行加窗，加窗后滤波器的冲激响应为

h(m)=(W(m-D)sinc(m-D),0≤m≤M-1。加窗后的分数时延滤波器的时延精确程度与理想分数时延滤波器非常接近。